학교에서 들은 프로그래밍 언어론 강의 내용을 복습하면서 작성한 글입니다.
March 26, 2024 4:17 PM
Semantics (의미)
작성된 수식, 문장 혹은 프로그램의 의미 정하기
- 프로그램이 어떻게 동작하는가!
- semantics가 필요한 이유
- 프로그래머 - 문장의 의미 알아야함
- 컴파일러 작성자: 언어 구조가 하는 것 정확히 알아야함
- correctness 증명
- 컴파일러 생성기 가능
- 디자이너는 모호함, 불일치 감지
- 종류
- operational semantics : 시뮬레이션
- denotational semantics : 수학적 함수 기반
- axiomatic semantics : 공리(반드시 참이 되는 명제) 기반
Operational Semantics
- 프로그램의 동작, 실행 과정을 정의: 프로그래밍 문장 실행하여, 기계(register, memory) 의 state(상태)의 변화를 통해 문장의 의미를 정의
- high-level 언어 작동 시 가상머신 필요
- 문제
- hardware pure interpreter: 비용⬆️
- software pure interpreter: 특정 컴퓨터의 특성이 내용 이해하기 어렵게 만들 수 있고, 특정 기계에 의존해, 다른 기계에서는 동작하지 않을 수도 있음
→ 대안: 시뮬레이션 이용
- build translator (source code→ machine code)
- build simulator
- manual, textbook, teaching등 비공식적으로 사용되면 좋다 but 공식적으로 사용되면 매우 complex
Denotational Semantics
- 의미를 명확하게, 수학적 방식(=함수 형태)으로 표시하자.
- 추상적, recursive 활용
- denotational specification 작성 방법
- 언어의 각 구성 요소에 대한 수학적 객체 정의
- 언어 요소와 수학적 객체 간의 함수 정의(각 요소에 매칭되는)
현재 state s는 선언된 모든 변수의 상태로 나타낼 수 있다.
s = {<i1,v1>,<i2,v2>,...,<in,vn>}
→ VARMAP이 변수 이름과 state를 주면, 해당 변수의 value를 주는 함수라고 하면
VARMAP(i_j, s) = v_j
Decimal Numbers 예시)

예) 1201
M(<120>’1’) 은 120을 숫자로 바꾼 다음 10을 곱해서 int를 내보내고 맨 끝자리 1 더함.
재귀를 활용해서 string character로 부터 10진수 decimal로
Expressions
정수(Z)와 {error}의 합집합으로 expressions(표현식) 매핑
- 표현식: 값이 될 수 있는 것, 값을 반환하는 것 (10진수, 변수, 이진 표현식-산술연산자+2개 피연산자 ..)
Assignment Statements(배정, 할당문)
표현식 반환 결과로 나온 값을 변수에 변경, 할당, 대입, 배정할 수 있는 연산문
- 이름을 갖는 특정 변수에 값을 바인딩하는 문장
Logical Pretest Loops
- define하는데 recursion 사용
- 반복문 시작 전에 조건 검사해서 반복 실행할지 결정 → 반복 실행되기 전에 루프 조건이 검사되므로 최소 한번은 루프의 몸체가 실행될 수 있음?
- 수학적 설명: recursion > iteration
Denotational Semantics 평가
- 프로그램의 correctness을 증명 가능(엄격)
- 언어 디자인에 도움
- compiler generation에 쓰임
- 사용자들에겐 너무 복잡
Axiomatic Semantics
Axiom(공리, 당연한 이치) → 논리표현으로 만들어서 이용
- precondition: 문장 앞에 오는 assertion, 만족 후 실행시켜라
- postcondotion: 문장 뒤에 오는 assertion, 실행 후 만족 조건
- weakest precondition: 가장 제약이 적은 전제 조건, 해당 문장을 실행하기 위해 필요한 가장 최소한의 조건
Program Proof Process
- 프로그램의 실행결과: postcondition
Form
{P} statement {Q}
example)
a = b + 1 {a > 1}
possible precondition: {b > 10} //b=3,4 인 경우 실행 X
weakest precondition: {b >0} //어느 경우에도 실행되는 가장 약한 조건
Assignment
- Rule of Consequence (결론 규칙)
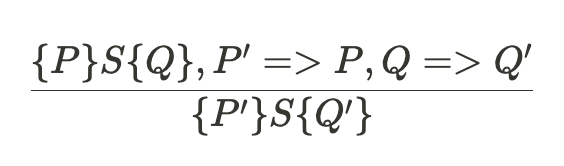
→ 의미: 프로그램의 일부인 문장 S가 변환된 전제 조건 P을 충족하고 실행된 후에 변환된 후에 후건 조건 Q을 보장한다면, 그리고 변환된 전제조건 P’이 원래 전제조건 P을 보장하고, 변환된 후건 조건 Q’가 원래 후건 조건 Q를 보장한다면, 이러한 전제와 후건 조건을 가진 변환된 프로그램의 일부인 문장 S는 변환된 전제조건 P’을 충족하고 실행된 후에 변환된 Q’를 보장
Sequences
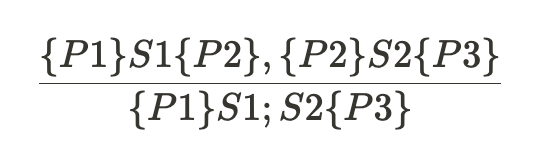
ex) y=3*x+1 , x=y+3, postcondition: {x<10}
→ 여기서 두번째 S의 precondition: y< 7 → 이것을 첫 번째 문장의 postcondition으로 사용시,
첫 번째 문장의 precondition 알 수 있음
3*x+1 <7 → x<2 이므로 {x<2}가 첫번째 문장과 전체 두 문장의 weakest precondition 이 됨
Selection
- if B then S1 else S2
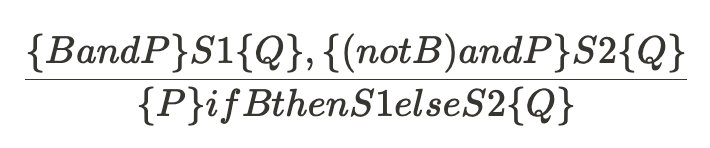
program 전체 실행하려면 then절과 else절에 모두 사용 가능한 전제 P가 필요
Loops
- loop 실행 시
- 변하는 것
- 변하지 않는 것: loop랑 상관없는 변수들(loop invariant)
{P} while B do S end {Q}
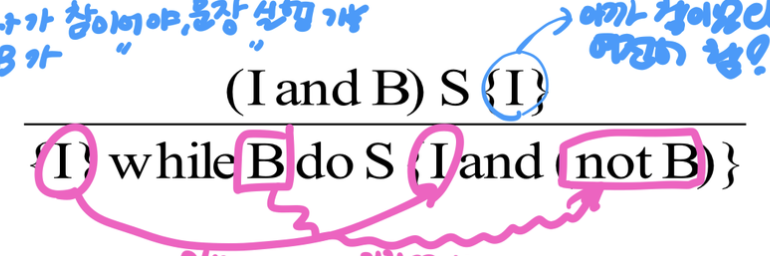
- loop invariant
- loop invariant 특성
- P => I : invariant는 초기에 참이어야함
- {I} B {I}: 루프의 조건 식 평가될 때, invariant는 변하지 않아야함
- {I and B} S {I}: 루프 본문 실행 뒤에도 invariant는 변하지 않아야함
- I, B 동시에 참일 때 실행
- I and (not B)) => Q: 루프 종료 시, invariant가 성립하고, 루프 조선은 거짓으로 빠져나와야함 loop 끝나면 post condition으로
- The loop terminates
- 너무 세면 loop가 실행되기 어려움
- invariant는 loop의 precondition과 postcondition 모두에 들어있기 때문에 충분히 약하게 만들어야 함 (그래야 실행)
- loop를 실행시키는 조건 B가 무조건 참이 되지 못하도록 충분히 강력해야함
- loop invariant 특성
Axiomatics Semantics의 평가
- 논리식→ 프로그램의 정확도(correctness) 증명이 편해짐
- Denotational Semantics는 사실 사용하기에는 어려움 → Operational Semantics 사용할 것임
- Denotational Semantics: state를 정의하고, state의 변화를 수식에 따라 엄격히
'CS > 프로그래밍 언어론' 카테고리의 다른 글
| [프로그래밍 언어론] Lex (0) | 2024.04.27 |
|---|---|
| [프로그래밍 언어론] Lexical and Syntax Analysis (0) | 2024.04.27 |
| [프로그래밍 언어론] Attribute Grammars (AGs) (0) | 2024.04.27 |
| [프로그래밍 언어론] BNF/EBNF (1) | 2024.04.26 |
| [프로그래밍 언어론] 개요 (0) | 2024.04.26 |