학교에서 들은 알고리즘 분석 강의 내용을 복습하면서 작성한 글입니다.
March 18, 2024 4:24 PM
Quicksort
- pivotting: 기준이 되는 것 중심으로 비교
- 중간값으로 pivot을 구하지 않는 이유: 중간값 구하는게 sorting만큼 오래걸림 → 포기 → 다 비슷하므로 → 맨 왼쪽 것을 pivot으로??
(교수님이 이렇게 설명햇음..)
- 중간값으로 pivot을 구하지 않는 이유: 중간값 구하는게 sorting만큼 오래걸림 → 포기 → 다 비슷하므로 → 맨 왼쪽 것을 pivot으로??
- pivot을 기준으로 pivot보다 작은 요소들은 왼쪽, 큰 요소들은 오른쪽에 있도록 (내부 순서는 신경X)
- pivot 제외한 왼쪽 리스트, 오른쪽 리스트를 다시 정렬
- 분할된 부분 리스트에 대해 recursion 하게
- Q(n) = Q(l) + Q(r) +(n-1)
- n-1: 나 빼고 다 보기
- divide-and-conquer ?
- 분할: 기준점을 중심으로 두개의 부분배열로 분할
- 정복: 부분배열 정렬
- 결합: 정렬된 배열들 합병
Algorithm
void quicksort (index low, index high)
{
index pivotpoint;
if (high>low){
partition(low, high, pivotpoint);
quicksort(low, pivotpoint-1); //왼쪽
quicksort(pivotpoint+1, high); //오른쪽
}
}
void partition (index low, index high, index pivotpoint)
{
index i, j;
keytype pivotpoint;
pivotitem = S[low];
j= low;
for (i=low+1; i <= high ; i++)
if( S[i] < pivotitem ){
j++;
exchange S[i], S[j];
}
pivotpoint = j;
exchange S[pivotpoint], S[low];
}
시간복잡도
worst case: 두 덩어리로 나눌 수 없을 때 (즉, pivot이 sort되어 있을 때)
- Q(n)=Q(0)+Q(n-1)+n-1 =Q(n-1)+Q(0)+n-1

- worst case 시간복잡도: n^2
Best case: 양쪽이 유사(동일)할 때, 가장 complexity ⬇️ = average case
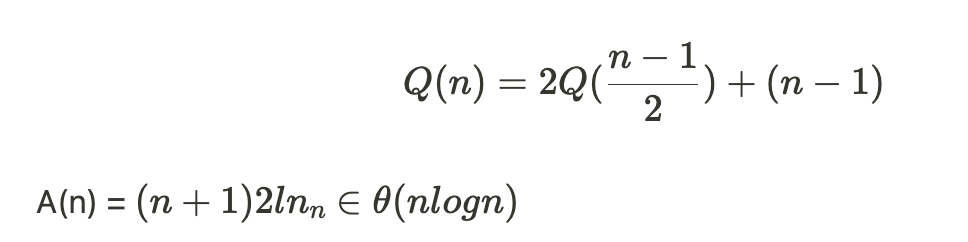
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] Dynamic Programming - Binomial Coefficient (0) | 2024.04.23 |
|---|---|
| [알고리즘] Divide and Conquer - Strassen’s Matrix Multiplication (0) | 2024.04.23 |
| [알고리즘] Divide and Conquer - Binary Search | Merge Sort (0) | 2024.04.23 |
| [알고리즘] Order (0) | 2024.04.23 |
| [알고리즘] 알고리즘 분석 개요 (0) | 2024.04.23 |